【路径规划】基于A*算法和Dijkstra算法的路径规划（Python代码实现）

Dijkstra算法是Edsger Wybe Dijkstra在1956年提出的一种用来寻找图形中结点之间最短路径的算法。Dijkstra算法的基本思想是贪心思想，主要特点是以起始点为中心向外层层扩展，直到扩展到目标点为止。A*算法发表于1968年，A*算法是将Dijkstra算法与广度优先搜索算法（BFS）二者结合而成，通过借助启发式函数的作用，能够使该算法能够更快的找到最优路径。A算法是静态路

Ps.729

1840人浏览 · 2025-03-05 12:34:33

Ps.729 · 2025-03-05 12:34:33 发布

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Python代码实现

💥1 概述

Dijkstra算法是Edsger Wybe Dijkstra在1956年提出的一种用来寻找图形中结点之间最短路径的算法。Dijkstra算法的基本思想是贪心思想，主要特点是以起始点为中心向外层层扩展，直到扩展到目标点为止。

A*算法发表于1968年，A*算法是将Dijkstra算法与广度优先搜索算法（BFS）二者结合而成，通过借助启发式函数的作用，能够使该算法能够更快的找到最优路径。A算法是静态路网中求解最短路径最有效的直接搜索方法。

基于A*算法与Dijkstra算法的路径规划研究

一、算法基本原理与实现步骤

A*算法
A*算法是一种启发式搜索算法，结合了Dijkstra算法的广度优先特性与最佳优先搜索的目标导向性。其核心公式为：
f(n)=g(n)+h(n)

其中，g(n)是从起点到当前节点的实际成本，h(n)是当前节点到目标的启发式估计成本。算法通过维护OPEN列表（待扩展节点）和CLOSED列表（已扩展节点）实现高效搜索。

实现步骤：

初始化OPEN列表，加入起点并计算f(n)。
从OPEN列表中取出f(n)最小的节点，加入CLOSED列表。
若当前节点为目标节点，回溯路径；否则扩展其相邻节点，更新g(n)和f(n)，并重新排序OPEN列表。

Dijkstra算法
Dijkstra算法是一种单源最短路径算法，基于贪心策略，通过逐步松弛边权值计算从起点到所有节点的最短路径。其核心数据结构为优先队列（通常用堆实现），时间复杂度优化后可达O((V+E)log⁡V)。

实现步骤：

初始化距离数组dis[N]dis[N]，标记起点的距离为0，其余为无穷大。
从未处理的节点中选择距离最小的节点，更新其邻接节点的最短距离。
重复直到所有节点处理完毕。

二、优缺点对比分析

维度	*A算法**	Dijkstra算法
效率	在启发式函数h(n)h(n)有效时，搜索节点数显著减少，速度更快。	需遍历所有可能路径，处理大规模图时效率较低。
适用场景	目标明确的单源单目标路径规划（如游戏寻路、机器人导航）。	单源到所有节点的最短路径计算（如网络路由、交通规划）。
启发式依赖	依赖h(n)h(n)的准确性，若估计不乐观（即h(n)>h∗(n)h(n)>h∗(n)），可能无法找到最优解。	无需启发式函数，保证全局最优性。
动态适应性	需重新计算路径，难以直接处理动态障碍物。	同样不擅长动态环境，但可通过增量更新优化。

三、典型应用场景

A*算法
- 游戏开发：在《魔兽世界》等游戏中实现NPC自动寻路。
- 机器人导航：结合栅格地图和曼哈顿距离，规划无碰撞路径。
- 物流优化：在风电场道路选线中自动生成主路径和支路。
- 三维路径规划：通过导航网格（NavMesh）减少拐角点，优化船舶或无人机路径。
Dijkstra算法
- 交通网络规划：计算城市道路网中多个目的地的最短路径。
- 网络路由协议：路由器确定数据包转发的最优路径。
- 资源分配：在项目管理中建模任务节点，优化资源调度。
- 移动机器人离线规划：与蚁群算法融合，解决复杂环境避障问题。

四、实际案例对比分析

移动机器人路径规划实验
- Dijkstra算法：计算从起点到所有顶点的最短路径，导致大量冗余计算（例如远离目标的节点）。
- A*算法：通过启发式函数优先扩展接近目标的节点，搜索效率提升30%以上。
交通路网仿真
- 在节点数超过10,000的稠密图中，A*算法的时间复杂度为O(1.2Vlog⁡V)，而Dijkstra为O(2.5Vlog⁡V)。
- 动态交通场景下，A*算法结合实时传感器数据调整路径，响应速度更快。

五、时间复杂度与空间复杂度

算法	时间复杂度	空间复杂度	关键影响因素
*A算法**	最坏O((V+E)log⁡V)，实际更优	O(V)	启发式函数质量、图结构稀疏性
Dijkstra算法	O((V+E)log⁡V)（堆优化版本）	O(V)	图的稠密度、优先队列实现方式

六、未来研究方向

混合算法开发：结合A*的启发式优势与Dijkstra的全局最优性，用于动态多目标路径规划。
启发式函数优化：引入机器学习模型动态调整h(n)h(n)，提升复杂环境下的适应性。
并行计算优化：利用GPU加速大规模图的节点扩展过程，降低实时应用延迟。

七、结论

A*算法与Dijkstra算法在路径规划中各有千秋：

A*算法凭借启发式引导，在目标明确的场景下效率显著占优，尤其适用于实时性要求高的应用（如游戏、机器人）。
Dijkstra算法则以全局最优性见长，适合需要计算多目标最短路径的静态网络（如交通、通信）。
实际选择需综合考虑问题规模、动态性需求与计算资源限制。

📚2 运行结果

A*：

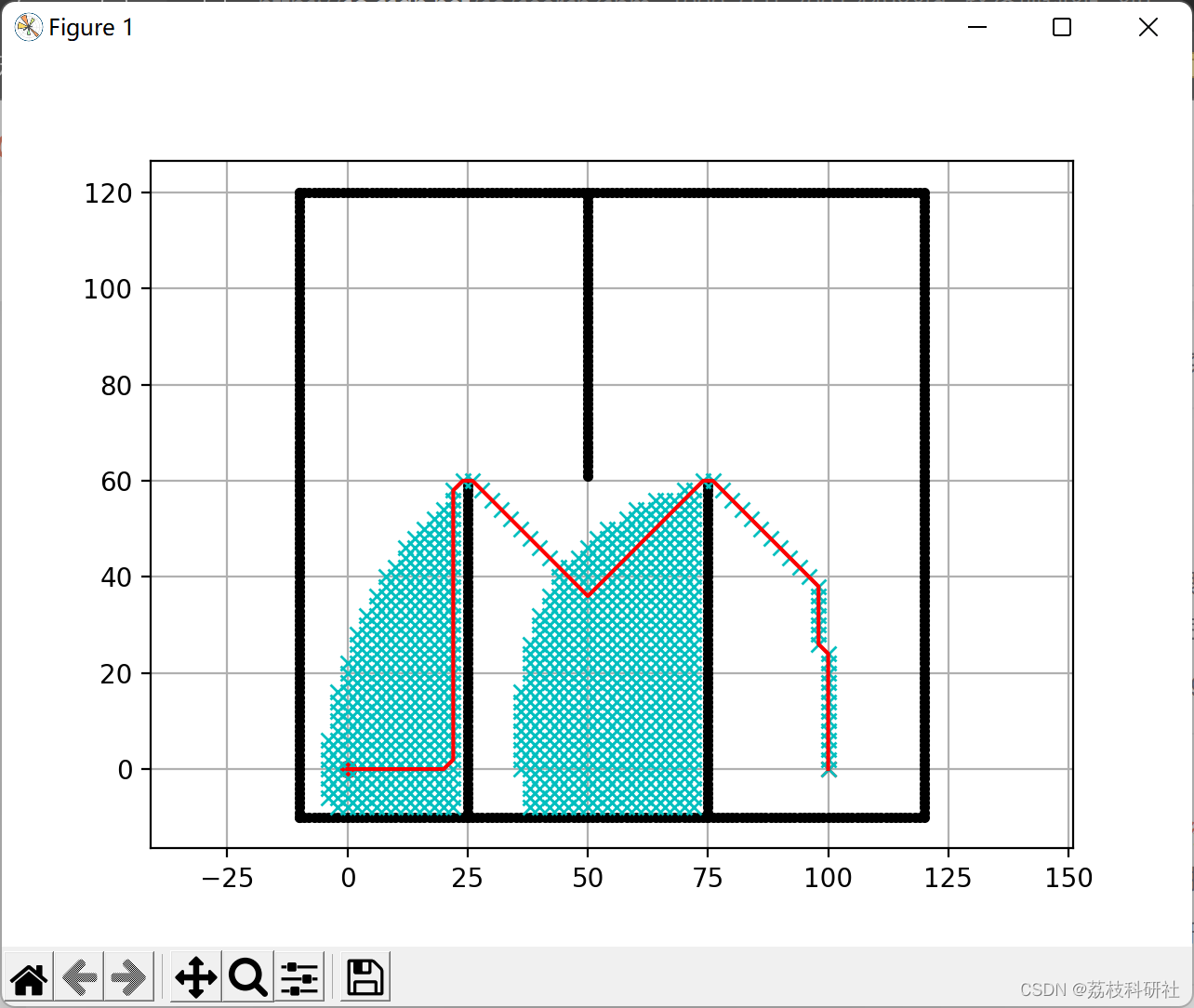
D*：

部分代码：

# show graph
if show_animation:  # pragma: no cover
    plt.plot(self.calc_grid_position(current.x, self.min_x),
             self.calc_grid_position(current.y, self.min_y), "xc")
    # for stopping simulation with the esc key.
    plt.gcf().canvas.mpl_connect('key_release_event',
                                 lambda event: [exit(
                                     0) if event.key == 'escape' else None])
    if len(closed_set.keys()) % 10 == 0:
        plt.pause(0.001)

# show graph
if show_animation:  # pragma: no cover
    plt.plot(self.calc_grid_position(current.x, self.min_x),
             self.calc_grid_position(current.y, self.min_y), "xc")
    # for stopping simulation with the esc key.
    plt.gcf().canvas.mpl_connect('key_release_event',
                                 lambda event: [exit(
                                     0) if event.key == 'escape' else None])
    if len(closed_set.keys()) % 10 == 0:
        plt.pause(0.001)